Se entiende por gestión de stocks el organizar, planificar y controlar el conjunto de stocks pertenecientes a una empresa.
La gestión de stocks regula el flujo entre las entradas de stocks y las salidas. La forma de regular el flujo de entrada es variando la frecuencia y el tamaño de los pedidos que se realicen a los proveedores. El control sobre el flujo de salida es mucho menor pues las condiciones son impuestas por los consumidores.[1]
La gestión de stocks ha de garantizar que siempre que un cliente solicite un producto este sea proporcionado. Lo ideal sería que el flujo de entrada fuese igual al de salida, pero esto no es materialmente posible, pues es necesario un tiempo para responder adecuadamente. Por lo tanto se ha de intentar que el nivel de stock sea mínimo, sin que se produzcan rupturas en la salida.[1]

Uno de los objetivos fundamentales de la gestión de stocks es conseguir satisfacer las necesidades de los clientes, garantizando la llegada de los productos en tiempo, forma y cantidad esperados. Sin embargo, este no es el único objetivo, pues es fundamental mantener un equilibrio entre lo anterior y los costes que derivan de la posesión de los stocks.[1]
Su función es la de servir de instrumento de regulación de toda la cadena logística, con el fin de conseguir un flujo de materiales continuo. Las siguientes funciones del stock nos las indican los autores ya nombrados anteriormente.[1]
La función del stock es conseguir:
- Compensar los tiempos de transporte necesarios para acercar el producto al cliente. Es necesario crear un stock cerca del consumidor ya que el momento y lugar en el que es demandado un producto suelen ser diferentes del sitio en que este producto se genera.
- Evitar rupturas del movimiento de materiales por cualquier suceso, como por ejemplo los desajustes en los sistemas de transporte.
Tipos de stocks
Los stocks pueden ser clasificados desde varios puntos de vista, de acuerdo a su función, a las actividades de la empresa y a la naturaleza de los productos.
La autora Francisca Parra Guerrero en su obra Gestión de Stocks[2] considera útiles para la gestión de existencias las siguientes clasificaciones:
Clasificación según la función que desempeñan los stocks en la empresa
1. Stock de seguridad o de protección
Volumen de existencias que se mantiene en almacén superior al necesario para el funcionamiento normal de la empresa que se constituye como protección frente a la incertidumbre de la demanda y del plazo de entrega del pedido.
Si existe un cierto tiempo entre el momento en que se hace el pedido al proveedor, y el momento en que éste llega al almacén, es decir, los aprovisionamientos no son instantáneos, entonces es indispensable prevenir un cierto numero de existencias para hacer frente a la demanda o salidas de almacén, durante el plazo de reposición. Si durante este espacio de tiempo la demanda es exactamente conocida, no hay ningún inconveniente en calcular las existencias necesarias para este fin. Sin embargo, si la demanda es aleatoria, entonces tendremos un factor de incertidumbre en la cantidad necesaria de existencias futuras para hacer frente a esta demanda. Es por esto por lo que a la hora de hacer un pedido, se requiere tener en almacén un número de existencias igual al consumo normal que tiene lugar durante el plazo de reposición, más una cierta cantidad, que aunque no esperamos salga del almacén antes de que llegue el nuevo aprovisionamiento, es de hecho necesaria para prevenir las posibles fluctuaciones imprevistas de la demanda.
También se requiere el aprovisionamiento en almacén de existencias de seguridad en el caso en el que la demanda es absolutamente conocida en todo momento pero existe ahora un factor de incertidumbre en el plazo de reposición. Si el plazo de reposición es aleatorio, es necesario contar con un cierto número de existencias, suficientes para atender la demanda durante los días en que el nuevo pedido puede tardar en llegar al almacén por encima del tiempo que se considera como plazo normal; si no fuera así existe el riesgo de que falten existencias para atender a las salidas ciertos días, si el nuevo pedido tarda en llegar un tiempo imprevisto.
Por último, las dos situaciones anteriores podrían darse de forma conjunta, es decir, que las salidas de almacén estén sujetas a una cierta oscilación y que el plazo de reposición sea un tanto incierto.
La cantidad del stock de seguridad depende de la variabilidad de la demanda y de la del plazo de entrega del pedido, y del riesgo de encontrarse sin existencias que la empresa está dispuesta a asumir. Evidentemente el riesgo de ruptura será menor cuanto mayor sea el volumen del stock de seguridad.
La efectividad de los almacenes donde sean necesarios los stocks de seguridad depende del cálculo de esté. Los parámetros que permiten estimar las fluctuaciones en el cálculo de las existencias de seguridad pueden medirse mediante distribuciones estadísticas.
2. Stock medio
Es el volumen medio de existencias que tenemos en el almacén durante un periodo de tiempo. Representa la inversión media que tenemos en existencias.
El nivel de stocks en almacén evoluciona entre un máximo, que coincide con la entrada de un pedido al almacén, y un mínimo, que refleja el volumen de stocks en el momento antes de tener lugar la llegada al almacén de un nuevo pedido. El stock medio es la medida aritmética de ambos extremos, para un solo plazo de aprovisionamiento (tiempo que media entre dos entradas consecutivas de almacén).
Si queremos calcular el stock medio dado para un periodo de tiempo superior a un plazo de aprovisionamiento, tenemos que tener en cuenta que no solo se habrán producido salidas, sino que se habrá producido más de una entrada, con lo que habrá que aplicar la media ponderada según el sistema de aprovisionamiento de que se trate.
- Pedidos en cantidades fijas y fechas fijas. Los tiempos que median entre dos llegadas consecutivas al almacén son uniformes y los stocks máximos y mínimos en cada ciclo son iguales, por lo que el valor del stock será constante e igual a la media aritmética simple del stock máximo y mínimo de un solo plazo de aprovisionamiento. Destacamos que, no es necesario mantener un stock de seguridad, pues todos los elementos que median en la gestión son totalmente cuantificables. Esto supone que el stock mínimo será cero, por lo que el stock medio será igual al volumen del lote a pedir Q, dividido por dos:
- Pedidos en cantidades fijas y fechas variables. Si el plazo de entrega es nulo, es decir los aprovisionamientos son instantáneos, los niveles de stocks máximos son todos iguales y los mínimos de existencias serán cero, por tanto el stock medio será también Q/2.
- Pedidos en cantidades variables y fecha fija. Si los pedidos se hacen siempre con la misma frecuencia pero por cantidades variables, o sea, que los plazos de aprovisionamiento son iguales, nos encontraremos con distintos niveles máximos de existencias en almacén, y, si la demanda es aleatoria, con distintos niveles mínimos. Para calcular en éste caso el stock medio calcularemos la media aritmética simple de todos los stocks máximos y mínimos habidos durante dicho período de tiempo T:
- Donde ai son los niveles máximos de existencias, bi los niveles mínimos de existencias, y n es el número de plazos de aprovisionamiento comprendidos en el tiempo al cual referimos el stock medio (T).
- Pedidos en cantidades variables y fechas variables. En este caso es evidente que, para cada plazo de aprovisionamiento, tendremos unos niveles máximos y mínimos de existencias distintos con los consiguientes stocks medios también diferentes. Además, como los plazos de aprovisionamientos también tienen una duración variable, habrá que cuantificar el stock medio global mediante una media aritmética ponderada:
- Donde ai y bi corresponden a los niveles de existencias máximo y mínimo respectivamente, ti son la unidades de tiempo que transcurren entre la llegada al almacén de dos pedidos consecutivos, y T es el período de tiempo total al cual referimos el stock medio, en la unidades de tiempo correspondientes.
3. Stock de anticipación
Se trata de stocks de producción estacional o periódica como es el caso de materias primas de las que hay que aprovisionarse en el momento en el que estás están disponibles. Pueden constituirse también para situaciones en las que es conveniente aprovisionarse en el momento en el que el precio del articulo es más bajo con la intención de especular con ellos, o para utilizarlos en periodos en los que el aprovisionamiento es más costoso, como por ejemplo en situaciones de huelgas.
4. Stock sobrante
Constituyen el stock sobrante todos aquellos artículos que estando en buen estado no son necesarios. Este inventario debe salir del almacén, bien sea utilizándolo de otro modo al que en principio estaba destinado, o bien, si es posible, devolviéndolo al proveedor, o si no hay otra solución, tirándolo. Estos artículos no deben ser abandonados indefinidamente en el almacén.
5. Stock activo
Este tipo de stock es conocido también como stock normal, stock cíclico o stock de trabajo.
Normalmente no se compran o producen artículos a medida que se van demandando, sino que se lanza una orden de pedido de un tamaño superior a las necesidades del momento, dando lugar a un stock que es consumido a lo largo del tiempo. Este stock sigue un comportamiento cíclico.
Este es el stock que abastece la demanda de la empresa en una situación normal de funcionamiento.
Clasificación según la naturaleza física de los productos
En la gestión de almacenes puede ser determinante la naturaleza física de los stocks. La autora Parra Guerrero hace esta clasificación desde dos puntos de vista:
Según la duración de la vida útil de los productos
-
- Perecederos
- No perecederos
- Artículos con fecha de caducidad marcada
Según el tipo de actividad de la empresa
-
- En empresas comerciales
-
- Artículos básicos. Productos que caracterizan a una empresa y que la incluyen en un sector determinado.
- Artículos obsoletos o pasados de moda. Artículos a los que no se dio salida en periodos de venta anteriores. Estos artículos han de dejar de ocupar un lugar en el almacén ya que esto conlleva un coste, por lo que habrá que encontrar la forma de darles salida.
- Artículos deteriorados o defectuosos. El volumen de este tipo de artículos en una empresa comercial no suele ser elevado ya que normalmente el proveedor suele hacerse responsable, sobretodo si el defecto es de fabrica. En caso contrario también es importante dar salida a estos artículos.
- Artículos complementarios. Formado por artículos que no son esenciales para la empresa comercial pero que sin embargo son necesarios para dar un mejor servicio al cliente.
-
- En empresas industriales
-
- Materias primas. Este tipo de existencias es necesario para abastecer el proceso productivo, si se agota la materia prima el proceso de producción se verá interrumpido. El ritmo de fabricación será el que marque las salidas del almacén de materia prima.
- Productos semi-acabados procedentes de los proveedores exteriores. La gestión de este tipo de existencias tiene las mismas características que las materias primas.
- Productos semi-elaborados, pero no procedentes de proveedores exteriores, sino de una fase del proceso productivo. Son productos que ya han sufrido parte de las operaciones de producción y están a la espera de entrar en otra fase para continuar el proceso de producción. Su venta no tendrá lugar hasta que se complete dicho proceso productivo. Este tipo de existencias ha de suponer unos costes mínimos pero a la vez su volumen a de ser el adecuado para cumplir con su objetivo, la continuidad del proceso productivo.
- Productos acabados . Son los artículos finales destinados bien al consumo final o a la venta.
- Repuestos. Todos aquellos artículos y piezas de maquinaria necesarias para solucionar averías.
- Recambio. Lo normal es que una empresa sea capaz de producir varios artículos, en la mayoría de los casos una misma máquina es utilizada para la producción de más de un tipo de artículo, pero para esto es común que halla que cambiar alguna pieza o componente de la máquina. Estas piezas y componentes constituyen el stock de recambio.
- Suministros industriales. Todo material necesario para el mantenimiento y buena conservación del equipo industrial.
Costes de la gestión de stocks
Los costes más relevantes que se tienen en cuenta en la gestión de stocks son:[3]
- Coste de aprovisionamiento:
- - Coste del pedido.
- - Coste de emisión de pedido.
- Coste de almacenaje.
- Coste asociado a la existencia de demanda insatisfecha.
Coste de aprovisionamiento
Es el coste total que tiene lugar cada vez que se hace un pedido de un artículo. Este coste se divide en dos:
- Coste del pedido: Es el resultado de multiplicar el valor unitario del artículo por el número de artículos de que consta el pedido. Este coste es variable, pues depende de la cantidad del artículo pedido.
- Coste de emisión del pedido: Este coste es fijo y será diferente dependiendo de si se trata de artículos comprados a un proveedor externo o si son pedidos de artículos manufacturados en la misma empresa.
En el primero de los casos el coste de emisión del pedido incluye varios costes, tales como: tiempo de personal administrativo, tarifas telefónicas y postales, inspecciones y operaciones de carga y descarga.
En el caso de artículos manufacturados por la propia empresa existen además de todos los costes anteriores, los costes asociados a la preparación de los equipos para el lanzamiento de la producción del pedido. Estos costes pueden incluir o no los costes asociados a la interrupción de la producción, dependerá de si es necesario o no interrumpir la producción para la preparación de los equipos.
Coste de almacenaje
Son todos aquellos costes que tiene la empresa como consecuencia de conservar una determinada cantidad de artículo en stock. Los factores que influyen en el coste de almacenaje pueden ser:
- Obsolescencia: Puede ocurrir que haya artículos en el almacén a los que no se llegue a dar salida debido a que se hayan producido cambios en los gustos de los consumidores, o bien, se haya producido una evolución tecnológica durante el tiempo en que el artículo ha estado almacenado.
- Robos y desperfectos: Durante el tiempo de mantenimiento de un inventario pueden darse condiciones tales que se pueda producir la pérdida de algunos artículos, como por ejemplo roturas accidentales, condiciones ambientales no adecuadas y robos.
- Seguros: Normalmente los inventarios están cubiertos por algún tipo de seguro.
- Almacén: Para mantener inventarios es necesario disponer de almacenes, así como del personal y equipos adecuados para el manejo de materiales.
- Capital: El coste de oportunidad del capital es el coste en el que se incurre al tener inmovilizado en inventario el capital correspondiente en vez de invertirlo.
Es normal que el coste de almacenaje se exprese como un porcentaje anual de la inversión en inventarios incluyendo los conceptos anteriores.
Coste asociado a la existencia de demanda insatisfecha
Este coste se produce cuando no es posible atender a la demanda debido a que cuando esta se produce no hay inventario en el almacén. Esta situación es conocida como rotura de stock.
El objetivo de la gestión de stocks
El objetivo de la gestión de stocks para un articulo individual debe dar respuestas a las siguientes preguntas básicas:[3]
-
- ¿Cuando debe lanzarse una orden de pedido de dicho artículo?
- ¿Qué cantidad del artículo debe pedirse en cada una de estas órdenes de pedido?
Clasificación de los sistemas de gestión de stocks
Los sistemas de gestión de inventarios se clasifican en modelos de situaciones de inventarios. El criterio de clasificación de estos modelos se hará en base al grado de conocimiento de la demanda.[3]
Pueden darse dos situaciones para el grado de conocimiento de la demanda:
-
- La demanda futura es conocida con exactitud, no existiendo incertidumbre en cuanto a su evolución. En este caso se dice que la demanda es conocida con certidumbre.
- En el periodo considerado la previsión de la demanda no garantiza un valor concreto, en la mejor de las situaciones, se espera un valor medio, alrededor del cual es previsible cierta variabilidad. En este caso se dice que la demanda es conocida en términos probabilísticos.
Modelos deterministas. Demanda independiente.
Los modelos deterministas son aquellos que suponen una demanda aproximadamente constante y conocida con certidumbre. Este modelo responde a la pregunta sobre el momento en el que hay que lanzar la orden de pedido. Como la demanda es conocida y no varía en el tiempo, será suficiente conocer el tiempo de espera para saber el momento exacto en que debe ser lanzada la orden de pedido.
Por lo tanto la pregunta que nos queda responder en los modelos deterministas es la referente a la cantidad de pedido. Para contestarla determinamos el llamado lote económico de pedido.
Lote económico de pedido
Para desarrollar un modelo simple vamos a considerar una serie de hipótesis:
- La demanda es continua a una tasa constante.
- Esta situación se prolonga en el tiempo indefinidamente.
- No hay restricciones en cuanto a cantidad de pedido, la capacidad de almacenamiento y el capital disponible.
- El plazo de entrega es nulo.
- No se permiten roturas de inventario.
- No se consideran descuentos en el precio de compra del articulo.
- Los costes se consideran invariables en el tiempo.
Aunque estas hipótesis son muy restrictivas, y es poco probable que existan situaciones de inventario que se ajusten a ellas simultáneamente, su consideración simplifica el análisis. La mayor utilidad de este modelo sencillo es que a partir de los resultados obtenidos permite desarrollar reglas de decisión para sistemas mas complejos y adaptados a situaciones reales.
En este modelo sencillo, por las hipótesis aceptadas, los costes que van a ser tenidos en cuenta son los de emisión de pedidos y el coste de almacenaje.
Variable y símbolos utilizados:
Cuando es lanzada una orden de pedido de un tamaño de Q unidades, como por hipótesis el aprovisionamiento es instantáneo, el nivel inventario alcanza inmediatamente dicho valor Q. Desde ese momento, al ser la demanda continua y a una tasa constante, se produce una disminución del nivel de inventario hasta que éste llega a cero, momento en el que se lanza una nueva orden de pedido, repitiéndose el proceso de forma recurrente. La evolución en el tiempo del nivel de inventario tendrá la forma característica de diente de sierra.
El coste anual de emisión de pedidos será:
Por lo tanto mientras mayor sea el lote, menor sera el numero de pedidos que habrá que hacer y en consecuencia los costes anuales de emisión de pedidos serán menores.
Mantener una unidad del artículo en el inventario durante un año supone un coste de r x c (unidades monetarias). El pedido se realiza en cantidades y fechas fijas, por lo que el stock medio es Q/2 unidades, y el coste anual de almacenaje es:
A medida que aumente el tamaño del lote de pedido, aumenta el coste de almacenaje.
El coste total anual del inventario será la suma de estos dos conceptos anteriores:
Fórmula de Wilson:
Llamada así en honor a R. H. Wilson. Esta formula nos da el valor del lote Q que hace mínimo el coste total. Se representa por Q* y se obtiene al derivar con
respecto a Q la expresión de CT e igualar a cero.
El coste total mínimo se obtendrá de sustituir el valor obtenido de Q* en la expresión correspondiente:
[editar] Lote económico de producción
Normalmente una orden de pedido es seguida de una orden de producción del articulo pedido, por lo que es necesario un cierto periodo de tiempo para completar dicha orden de producción. Durante este tiempo el artículo esta siendo producido y demandado. Para que este caso tenga sentido la tasa de producción, tiene que ser mayor que la tasa de demanda, ya que si no fuese así no existiría inventario en ningún momento.
Se define la tasa de producción, P, como el numero de unidades producidas en un periodo de tiempo generalmente un año.
Cuando el inventario se agota, punto A, se inicia la producción de la orden de pedido del lote Q. Se requiere un tiempo de producción Q/P. Durante este tiempo el inventario se va acumulando a una tasa P-D, por lo que cuando se acabe la producción del lote de tamaño Q se alcanzará el nivel máximo de inventario I (punto B), que es:
Desde este punto, el nivel de inventario decrece, como consecuencia de una demanda uniforme y constante, cuando las existencias se agotan el ciclo se inicia de nuevo.
Coste anual de emisión:
El stock medio:
Por lo que el coste anual de almacenaje es:
El coste total anual:
Podemos obtener de la misma forma que para el caso del modelo simple, el valor del lote óptimo que minimiza los costes:
Como era de esperar, para un aprovisionamiento instantáneo, P = ∞, obtenemos la formula de Wilson.
Descuentos por cantidad
En la práctica comercial es habitual la existencia de descuentos en función de las cantidades compradas, por lo que ha de considerarse a la hora de decidir sobre la cantidad artículos del pedido.
Normalmente se dan dos modalidades de descuentos: descuentos globales o totales y descuentos incrementales.
-
- Descuentos globales, los descuentos afectan a todas las unidades compradas.
- Por ejemplo, este tipo de descuento correspondería al siguiente caso: un suministrador le oferta al comprador la opción de comprar 1 000 unidades a un precio de 1 euro, si compra entre 1 001 y 2 000 unidades el precio de cada unidad será de 0,98 euros y si compra más de 2 000, el precio es de 0,95 euros la unidad. Para un pedido de 2 350 unidades, el precio será:
-
- Descuentos incrementales, en este caso el precio por unidad de articulo se establece por intervalos.
- Para este caso el ejemplo sería el siguiente: el suministrador oferta al comprador comprar 1 000 unidades a 1 euro la unidad, si compra entre 1 001 y 2 000 unidades el precio será de 1 euro la unidad para las primeras 1 000 unidades y de 0,98 euros la unidad para las unidades de 1 001 en adelante, si el pedido del comprador es superior a 2 000 unidades el proveedor le ofrece el articulo a 0,95 euros la unidad a partir de la unidad número 2 000. Es decir, para un pedido de 2 350 unidades, el precio será:
![]()
Modelos no deterministas. Demanda dependiente.
Los modelos no deterministas son aquellos que suponen que las ventas reales para un determinado período de tiempo varían aleatoriamente alrededor de un valor medio aproximadamente constante. El factor a tener en cuenta en este modelo es la variabilidad de la demanda durante el tiempo de espera o plazo de reaprovisionamiento, de forma que permita determinar el stock de seguridad acorde con el nivel previamente fijado de servicio a los clientes.
En los modelos no deterministas es necesario responder a las dos preguntas de cuánto y cuándo pedir para cada artículo que se mantiene en almacén. Según sea el sistema de información, previamente adoptado, un sistema de revisión continua o de revisión periódica, podemos clasificar los sistemas de gestión en dos grandes grupos:
- Sistemas de revisión continua: Sistemas de información en los que el estado del inventario se actualiza inmediatamente después de cada transacción (entrada o salida del artículo en el inventario). El sistema de gestión de inventarios más sencillo y fácil de implantar para este tipo de sistema de información es el sistema de lote óptimo-punto de pedido.
- Sistemas de revisión periódica: El estado del inventario del artículo es conocido cada cierto tiempo, llamado periodo de revisión. El sistema de gestión de inventarios más representativo para este tipo de sistema de información es el sistema de revisión periódica-nivel de pedido.
En estos modelos es necesario estimar la demanda durante el periodo de reaprovisionamiento, estimando la demanda media durante dicho plazo y una medida de las desviaciones previsibles en torno a este valor medio. La demanda más significativa es la demanda durante el plazo de reaprovisionamiento, ya que es en este periodo de tiempo es el que existe riesgo de rotura de stocks. Es para prevenir esta situación para lo que se tiene el stock de seguridad.
La clasificación ABC
En la mayoría de los casos, se caracterizan las situaciones de inventario por tener una gran cantidad de artículos mantenidos en stock. La clasificación ABC de los artículos que están en inventario es un instrumento eficaz para abordar la resolución de los problemas de inventario.[3]
En los sistemas de inventario con un gran número de artículos se observa que una pequeña porción de ellos representa un elevado porcentaje del valor monetario anual acumulado, y una gran fracción de artículos representa un pequeño porcentaje de dicho valor monetario anual total. Se establece una clasificación de los artículos en tres categorías:
- A (los más importantes)
- B (importancia intermedia) y
- C (los menos importantes).
Según se ha definido esta clasificación, un artículo caro con poco movimiento puede ser clasificado en la misma clase que un artículo de poco valor unitario y mucho movimiento. Como el objetivo es desarrollar reglas homogéneas de gestión para cada grupo de artículos, es lógico distinguir entre estas dos situaciones, diferenciando entre artículos de alto o bajo movimiento en términos de la demanda durante el tiempo de espera.
- La mayor atención será prestada a los artículos de clase A. La mayoría de las veces estos artículos representan entre un 3 y un 10 por ciento del total de los artículos del inventario y suponen más del 50 por ciento de la demanda total anual expresada en términos monetarios.
- Los artículos de clase B componen una clase numerosa, ya que normalmente más del 40 por ciento de los artículos representan la mayor parte del valor monetario de la demanda anual restante.
- Los artículos de clase C representan el resto del valor monetario de la demanda. Para estos artículos, las reglas de decisión deben ser lo más simples posibles. Normalmente se recomienda disponer de un stock de seguridad alto para estos artículos poco importantes, con la intención de minimizar los inconvenientes causados por una rotura de inventario.




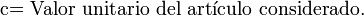
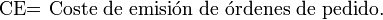



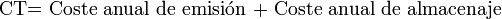
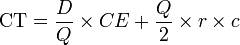
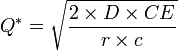


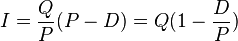

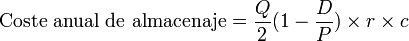


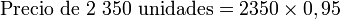
Escribir comentario